Yes raster is faster, but raster is vaster,
and vector just seems more correcter.
C.D. Tomlin (1990)
Allgemeines
Während die vektororientierte Datenstruktur mehr oder weniger direkt die linien- und flächenhaften geometrischen Eigenschaften der zu modellierenden Entitäten widerspiegelt, finden wir beim rasterorientierten Ansatz eine ganz andere Repräsentation von Objekten: Die geometrischen Grundstrukturen werden in einzelne Rasterpunkte (Bildelemente, Pixel) zerlegt. Die Rasterelemente sind in der Regel quadratisch geformt und meist auch von identischer Größe.

Grundtypen der rasterbasierten Modellierung
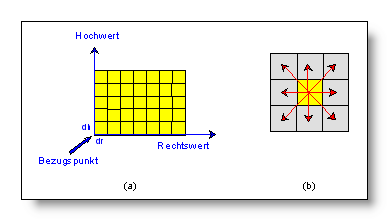
Hat die Entität eine volumenhafte Ausprägung, kann die Abbildung durch Volumenelemente (volume elements, voxels) erfolgen (Abb. (b)). Kontinuierliche Werteverläufe, wie Geländehöhen, Niederschlagswerte oder Lärmimmissionen, können diskretisiert als Rastermatrix approximiert werden. Logisch zusammenhängende Information (z.B. Flächennutzung, Geländehöhe) wird man in der Regel in einer Rastermatrix (Datenebene, Layer) ablegen, während andere Daten weiteren Datenebenen zugewiesen werden (Abb. (c)).
Die Rasterstruktur selbst, versehen mit einer Metrik, definiert die Lage der Objekte im Raum (siehe Abb.). Der geometrische Bezug der Rasterpunkte ermöglicht so auf einfache Weise, räumliche Beziehungen der Elemente untereinander zu untersuchen.
Thematische Auswertungen, wie z.B. das Überlagern verschiedener Datenebenen, werden sehr effizient durchgeführt.
Jedem Rasterelement ist ein Zahlenwert (Klassennummer, Graustufe) zugeordnet, dem im Einzelfall unterschiedliche Semantik (Bedeutung) zukommt. In den nachfolgenden Abbildungen sind einige Möglichkeiten dargestellt:
a) Eine Klassennummer kann als identifizierendes Kennzeichen das Rasterelement als Teil einer bestimmten Fläche kennzeichnen (z.B. eines Grundstücks).

b) Die Klassennummer ist klassifizierendes Attribut. In diesem Fall repräsentiert der Zahlenwert die Zugehörigkeit eines Gewässers zu einer gewissen Ordnungsstufe.

c) Die Klassennummer gibt nicht direkt ein Attribut wieder (wenn beispielsweise nur ganzzahlige Werte als Klassennummer möglich sind, der Wertebereich des Attributs jedoch reell ist). Der Attributwert wird erst durch eine Abbildung der Klassennummer auf den Attributwertebereich (Reklassifizierung) ermittelt.

d) Sollen mehrere Attribute mit den Entitäten verknüpft werden, dient die Klassennummer als Zugriffsschlüssel auf eine Attributtabelle.

Die beschränkte geometrische Auflösung eines Rasterpunktes (vgl. Abb. ) und die durch die häufige Verwendung ganzzahliger Zahlenwerte eingeschränkte Quantisierung der Information (Abb.) bedingen eine begrenzte Genauigkeit rasterbasierter Information.
Datenkompression
Für effizienten Zugriff und Reduzierung des Speicherplatzbedarfs gibt es verschiedene Methoden der Datenkompression und -verwaltung, von denen im folgenden Bitreduktion und Lauflängencodierung vorgestellt werden; der Quadtree-Zerlegung wird ein ausführlicherer Abschnitt gewidmet.
Bitreduzierung: Die physikalische Speicherung sollte aus Speicherplatzgründen der Quantisierung der in der jeweiligen Datenebene abgelegten Information entsprechen. Ist etwa nur eine Information abgelegt (z.B. „Gewässer“ bzw. „kein Gewässer“), so ist die Speicherung mit 1 bit pro Rasterelement ausreichend (binäre Karte). Die Verwendung solcher „Binärbilder“ erlaubt darüber hinaus die sehr effiziente logische Verknüpfung unterschiedlicher Datenebenen.
Lauflängencodierung: Eine weitere Möglichkeit der Datenkompression stellt die Lauflängencodierung (run length code) dar. Hierbei werden in jeder Zeile Rasterpunkte mit gleichem Grauwert zusammengefaßt und Startpunkt und Länge der so gebildeten Punktfolgen abgespeichert.
Die Effektivität der Lauflängencodierung ist abhängig von der Struktur der zu komprimierenden Datenebenen. Bei ausgeprägt homogenen Daten ist ein hoher Kompressionsgrad zu erreichen, bei sehr inhomogenen Daten ist eher eine Vergrößerung des Datenvolumens zu erwarten.
Die Quadtree-Zerlegung
Das Prinzip der Quadtree-Zerlegung beruht auf einer rekursiven Zerlegung von Bildbereichen und Zusammenfassung homogener Bereiche (vgl. Abb.). Das Gitter wird schrittweise bis zu einer gewünschten Auflösung verfeinert, bis jede Gitterzelle eine homogene Fläche repräsentiert.
Die Zelle wird dann zusammen mit ihrem charakterisierenden Merkmal (Klassennummer) und einer einzigen Koordinate gespeichert, die sich auf die dabei entstandene, baumförmige Datenstruktur (den Quadtree) bezieht.

Aufgrund ihres Aufbaus ist die Quadtreestruktur ein sehr guter Kompromiß zwischen Vektor- und Rastermodell, auch kann sie viele Vorteile dieser Methoden in sich vereinigen:
- Variable Auflösung: Die Quadtreestruktur nähert durch die Anpassung der Zellgröße an die räumliche Variation der Daten die Genauigkeit der Vektordatenstruktur an. Im Quadtree können Daten unterschiedlicher Auflösung überlagert werden; die Verknüpfung geschieht einfach auf verschiedenen Auslösungsstufen. Das Ergebnis bewahrt jedoch den Detaillierungsgrad der einzelnen Datensätze.
Bei der Auswahl eines Rastersystems ist zu prüfen, wie bei der Verknüpfung von Datenebenen unterschiedlicher geometrischer Auflösung verfahren wird.
Geringer Speicherplatzbedarf: Wird die räumliche Auflösung verdoppelt, wächst der Speicherbedarf nur linear. - Geringer Speicherplatzbedarf: Wird die räumliche Auflösung verdoppelt, wächst der Speicherbedarf nur linear.
- Hohe Effizienz: Algorithmen für Flächenberechnung oder komplexe Verschneidungen reduzieren sich in der Quadtreestruktur auf einen Vergleich der Klassennummern in den verschiedenen Auflösungsstufen der beteiligten Quadtrees mit einem einmaligen Durchlauf der Datenstruktur. Bei diesen Auswertungen kann die explizite Lageinformation (Rechtswert, Hochwert) unberücksichtigt bleiben, die logische Anordnung der Zellen innerhalb der Datenstruktur genügt. Dadurch sind sie insbesondere für nachbarschaftsbezogene Auswertungen geeignet.
- Bildpyramiden mit unterschiedlicher Auflösung haben insbesondere durch die effiziente Nutzung von Rasterdaten in Online-Mapping-Tools wie Google Maps eine große Bedeutung gewonnen. Dabei werden in Abhängigkeit von der jeweiligen Zoomstufe unterschiedliche Rasterdateien (tiles) geladen und zur Anzeige gebracht. Den einzelnen Rasterdateien liegt dabei eine vergleichsweise einfache Namenskonvention zugrunde, wie hier ersichtlich.

Kachelstruktur in verschiedenen Zoomstufen, aufgezeigt am Beispiel Google Maps (Quelle: unbekannt)
Auswerteverfahren
Mit Rasterdaten lassen sich viele der mit Vektordaten möglichen Auswerteverfahren ebenfalls durchführen. Daneben sind sie insbesondere für Verfahren interessant, die die Nachbarschaft einbeziehen (Bonham-Carter 1994).
Ableitung von Statistikparametern: Für einen Rasterdatensatz werden statistische Parameter wie Mittelwert, Standardabweichung, Extremwerte und Häufigkeitsverteilung bestimmt.
Nachbarschaftsbezogene Auswertungen: Für die Nachbarschaft werden beispielsweise die acht am nächsten gelegenen Rasterelemente in die Auswertung einbezogen, um statistische Parameter wie Entropie und Varianz abzuleiten.
Inkrementelle Operatoren: Ergebnisse eines Analyseschritts werden an die benachbarten Rasterelemente weitergegeben. Verfahren dieser Kategorie sind die Bestimmung von Einzugsgebieten und die Ableitung von Kostenoberflächen.
Auswertungen von Höhenmodellen: Aufbauend auf einem Raster digitaler Geländehöhen sind u. a. folgende Analysen möglich:
- Hangneigung, Exposition und Hanglänge,
- Reliefenergie,
- Sichtbarkeitsuntersuchungen.

Rasterdaten als Schwarz-Weiß-Schummerung mit Höhenlinien und überlagerter Straßenkarte (hier Beispiel Tegernsee), Quelle: http://www.wenninger.de/produkte/img/DGM(sw)BadWiessee.jpg)
Weitere Einsatzmöglichkeiten
Neben der Möglichkeit, Daten selbst in Rasterform zu erfassen, zu speichern und auszuwerten, gibt es im GIS-Bereich eine Reihe weiterer Möglichkeiten der Nutzung rasterbasierter Daten:
- Archivierung analoger Vorlagen: Die Überführung analoger Unterlagen, wie Skizzen, Photos oder Verträge, in ein digitales Format geschieht mit Hilfe spezieller Geräte zur Analog-Digital-Wandlung (Scanner). Sinnvoll ist diese Vorgehensweise, wenn mehrere Nutzer über Netzwerk direkt auf die Daten zugreifen können. Bei allen Archivierungsansätzen ist es zwingend notwendig, ausreichend beschreibende Daten zu den Rasterdaten zu erfassen, um einen gezielten Zugriff zu ermöglichen. Liegen zu GIS-Objekten Archivdaten vor, ist bei den Objekten selbst ein Verweis auf die Archivinformation zu führen. Entsprechende Zugriffsverfahren sind in die GIS-Anwendung zu integrieren.
- Bilddokumentation: Zum Festhalten des Zustandes unserer Umwelt zu einem bestimmten Zeitpunkt (z.B. Bauwerksfassade, Leitungen im offenen Graben, Kanalinspektion) ist es möglich, Photographien oder Videosequenzen als Rasterdaten in das System zu integrieren.

Verknüpfung von Geoinformation und photographischer Dokumenation
- Planerstellung: Karten und Pläne können als reine Rasterdaten oder in Kombination mit Vektordaten zusammengestellt, redaktionell bearbeitet, verwaltet und ausgegeben werden. Typische Anwendungen sind Luftbild-, Orthophoto- oder Satellitenkarten sowie topographische Karten.
- Hintergrundinformation: Gescannte Karten oder Luftbilder können als Hintergrundinformation für vektorielle Information den räumlichen Bezug erleichtern.

- Digitalisiergrundlage: Karten werden gescannt und dienen als Grundlage für eine manuelle oder automatisierte Digitalisierung am Bildschirm.

Rasterdatensatz (Orthophoto) als Digitalisierungshintergrund
Bewertung der Rasterdatenstruktur
Als Vorteile der Rasterstruktur sind zu nennen:
- Rasterdaten weisen eine identische Struktur für punkt-, linien- und flächenförmige Objekte auf. Somit können vielfach einheitliche Konzepte und Verfahren angewandt werden.
- Kontinuierliche Oberflächen, wie z. B. Temperatur, Geländehöhe, Übergänge zwischen verschiedenen Bodenarten, können adäquat modelliert werden.
- Verschiedene Datenquellen – insbesondere im Bereich der Fernerkundung und den daraus abgeleiteten Informationen – liegen rasterbasiert vor und brauchen nicht gesondert digitalisiert werden.
- Weitere Datenquellen können sehr wirtschaftlich über einen Scan-Prozeß für die Verarbeitung in einem rasterbasierten GIS erschlossen werden.
- Überlagerungen und logische Auswertungen sind einfach, da alle Datensätze in einer Gitternetzstruktur vorliegen. So ist es bei der Verknüpfung von Daten meist nur noch erforderlich, den Inhalt der betreffenden Gitterzelle zu untersuchen.
- Die relativ begrenzte Anzahl von Datenformaten erleichtert die Datenumsetzung.
- Verschiedene Analyseoperationen lassen sich nur effizient mit Rasterdaten durchführen.
Folgende Aspekte der Rasterstruktur sind jedoch ebenfalls zu beachten:
- Die Rasterdarstellung eines Objekts ist eher gröber als es der realen Welt entspricht.
- Rasterbasierte Datenbanken werden sehr groß und wachsen (bei Verzicht auf Kompressionsverfahren) quadratisch mit der Rasterauflösung. Es stehen jedoch durch spezielle Komprimierungsverfahren für viele GI-Systeme Erweiterungen zur Verfügung, die auch sehr große Rasterdatenbestände (bis zu Gigabyte- oder Terabyte-Bereich) verfügbar machen können. Auch spezielle Serveranwendungen zur Rasterdatenbereitstellung und -analyse werden angeboten (Rasterserver, Image-Server).
- In manchen Systemen müssen alle Daten, ganz gleich welchen Ursprungs oder von welcher Genauigkeit sie sind, mit identischer Auflösung gespeichert und ausgewertet werden.