• Grundbegriffe
• Bäume, planare Graphen
• Auswerteverfahren
• Einfache, weitgenutzte vektorielle Strukturierungsansätze
• Verknüpfung mit Attributdaten
• Bewertung

Grundbegriffe

Graphik-Basisinhalte – Graphische Primitive

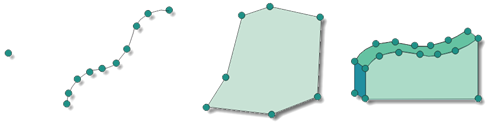
Führen wir uns nochmals Pläne oder technische Zeichnungen vor Augen, können wir die Inhalte der Zeichnung zunächst als eine Ansammlungen von verschiedenen graphischen Elementen (sogenannter graphischer Primitive) wie Punkten, Linien und gefüllten, umrandeten Flächen deuten:

In diesem einfachen Fall werden Linien und Flächenumrandungen durch eine (verbundene) Folge von Stützpunkten dargestellt (siehe Abbildung), denen wir erst aufgrund unserer geschulten Wahrnehmung eine Bedeutung – beispielsweise „Fläche“ – geben. Die Daten selbst kennen in dieser einfachen Strukturierungsform ihren Zusammenhang nicht. Aufgrund ihrer zufälligen Lage und Linienhaftigkeit spricht man umgangssprachlich auch von Spaghetti-Daten.

Topologie

Die Modellierung geometrischer Eigenschaften in einem GIS kann und muss abhängig von der Anwendung darüber hinausgehen. Ein wesentlicher Begriff in diesem Zusammenhang ist die Topologie der Daten. Die Topologie untersucht Eigenschaften, die bei stetigen (topologischen) Abbildungen unveränderlich sind, wozu auch die in der Geodäsie üblichen Transformationen zu zählen sind (FRANK 1983). Diese Eigenschaften sind per se unabhängig von der genauen geometrischen Lage der Objekte. Während das Beachten topologischer Bedingungen und Beziehungen (beispielsweise der Tatsache, dass eine Fläche durch mehrere, zusammenhängende Linien umschlossen wird) eher unbewusst im Rahmen der menschlichen Interpretation und im Kontext der entwickelten und gebräuchlichen kartographischen Techniken und Darstellungsarten geschieht, ist bei IT-gestützter Verar-beitung von Daten explizit auf Einhaltung topologischer Eigenschaften zu achten.

Topologische Strukturen und die damit verbundenen Auswertemöglichkeiten sind im GIS-Bereich nahezu ausschließlich für zweidimensionale Abbildungen entwickelt worden. Bei dreidimensional geprägten Objekten („3D-GIS“) besteht im GIS-Sektor noch Bedarf an wissenschaftlicher Untersuchung und praktischer Realisierung, beispielsweise bei Gebäudeinformationssystemen und bei 3D-Stadtmodellen (COORS 2005, KOLBE 2011, CHU et al.2012). Liegt der Schwerpunkt eines GIS-Einsatzes auf der dritten Dimension oder oder auf der Modellierung sich zeitlich ändernder Phänomene, schränkt sich die Auswahl der marktverfügbaren Systeme stark ein.

Topologische Grundbegriffe

Vor der Beschreibung dieser topologischen Bedingungen, wie sie auch in verschiedenen Systemen ganz oder teilweise realisiert sind, seien einige Definitionen gegeben. Für die Beschreibung topologischer Phänomene werden die Bezeichnungen

• Knoten für einen Punkt,
• Kante für die Verbindung zwischen zwei Knoten

verwendet. Wichtige Beziehungen zwischen ihnen sind:

• Inzidenz: Eine Kante beginnt und endet in einem Knoten.
• Adjazenz: Zwei Knoten sind durch eine Kante verbunden.

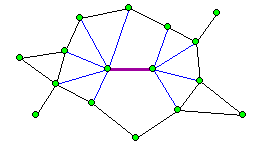
Die blau markierten Kanten sind adjazent zu der lilafarben markierten Kante.

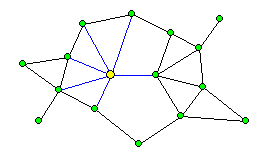
Die blau markierten Kanten sind adjazent zu dem gelb gekennzeichneten Knoten.

In einem Knoten können beliebig viele Kanten beginnen oder enden. Er ist Träger metrischer Information (Koordinaten). Zwei Punkte, deren Distanz Null ist (idealer Weise), sind identisch und bilden einen Knoten (Eindeutigkeit von Knoten). Einem Knoten können somit mehrere Punkte der Wirklichkeit entsprechen; die entsprechenden Bedeutungen (z.B. Grenzpunkt und gleichzeitiger Gebäudepunkt) sind zu vermerken. Änderungen der Koordinaten eines Knotens wirken sich automatisch auf alle inzidierenden Kanten aus.

Die mit den Kanten verbundenen Geometrien tragen Informationen über die Form (geradlinig, gekrümmt). Zwischenpunkte auf Kanten werden nicht als Knoten betrachtet; sie dienen lediglich der Bestimmung der Form). Somit kann eine Kante auch prinzipiell eine Kombination von Geradenstücken, Kreisbögen oder Kurven höherer Ordnung (beispielsweise von Splinebögen) sein.

Die beiden Kanten besitzen unterschiedliche Form, inzidieren jedoch mit denselben Knoten.

Zwei planare Graphen unterschiedlicher Geometrie können dennoch topologisch identisch sein.

Somit kann eine Kante auch prinzipiell eine Kombination von Geradenstücken, Kreisbögen oder Kurven höherer Ordnung (beispielsweise von Splinebögen) sein.

Für Kanten gilt, daß an einer Stelle des Raumes nur eine Kante gleicher Form existieren darf. Laufen also beispielsweise Kanten direkt nebeneinander her, so sind sie, eventuell unter Aufspalten der bisherigen Kanten und Neubildung von Knoten, miteinander zu verschmelzen. Die Bedeutung der Kantenstücke (z.B. Flurgrenze, Gebäudegrenze) ist, wie dies bei der Automatisierten Liegenschaftskarte der Fall ist, im Sinne einer Mehrfachbedeutung des Kantenstücks festzuhalten.

Bedeutung bei einer Systemauswahl

Bei der Systemauswahl muß davon ausgegangen werden, daß nicht jedes System alle Kantenformen (insbesondere Kreis- oder Splinebögen) verarbeiten und speichern kann. Ist diese Eigenschaft in einem System nicht gegeben, wird man diese gekrümmten Linien durch eine Reihe von geradlinig verbundenen Stützpunkten approximieren müssen. Dies kann ein Ausschlußkriterium sein, beispielsweise wenn die Forderung besteht, Flurstücksgrenzen durch Geraden und Kreisbögen abzubilden.

Beim Datenaustausch sind noch andere Aspekte von Bedeutung. Kreisbögen sind oftmals durch unterschiedliche Definitionsgrößen festgelegt, so daß geometrische Umrechnungen nötig werden. Kurven höherer Ordnung werden häufig systemabhängig mathematisch modelliert, so daß die Übernahme von Daten erschwert wird.

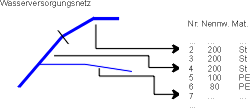
Bäume, planare Graphen

Aufbauend auf den Primitiven Knoten und Kante lassen sich komplexere geometrische Grundgebilde aufbauen, von denen im Zusammenhang mit GI-Systeme Bäume sowie planare Graphen von Bedeutung sind.

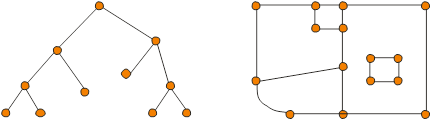
Bäume sind geeignet, um beispielsweise ein Gewässernetz zu beschreiben. Bei planaren Graphen liegen die Kanten zyklisch verbunden vor; sie können zur Beschreibung von flächenhaften Strukturen (Grundstücken, Nutzungsarten) verwendet werden. Ein von Kanten begrenztes Gebiet wird Fläche oder Masche genannt.

Die Abbildung zeigt ein Beispiel für einen planaren Graphen, an dem neben den zuvor genannten Bedingungen folgende Eigenschaften deutlich werden: Kanten schneiden sich nicht, jede Kante grenzt zwei verschiedene Teilflächen voneinander ab; eine Fläche kann wiederum Flächen enthalten (Inklusion), wie wir es beispielsweise von Flurstücken mit darin eingeschlossenen Enklaven her kennen.

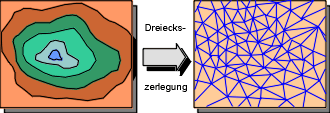
Einen Sonderfall stellt die in nebenstehender Abbildung gezeigte Bildung von vermaschten Dreiecksnetzen dar (triangulated irregular network, TIN). Diese werden verwendet, um Oberflächen, beispielsweise des Geländes, durch zusammenhängende Dreiecke zu modellieren.

Eine weitere Zerlegung des Raumes bieten Voronoi-Diagramme, auch Thiessen-Polygonen oder Dirichlet-Zerlegung genannt (vgl. Abbildung).
Dabei wird der Raum in unregelmäßige Teilflächen zerlegt. Jede Teilfläche wird durch genau ein Zentrum bestimmt und umfasst alle Punkte des Raumes, die näher an dem Zentrum der Teilfläche liegen als an jedem anderen Zentrum.

Die Beziehung von Knoten, Kanten und Maschen kann in DV-Systemen durch topologische Datenstrukturen beschrieben werden, wie sie sich in verschiedenen Systemrealisierungen und Austauschformaten finden. Beispielsweise kann die sofortige Prüfung und Bildung topologischer Beziehungen im Zuge der Datenerfassung ein effizientes Arbeiten ermöglichen und ein konsistentes Ergebnis sichern helfen. Für eine Systemauswahl stellt die Führung der Topologie bereits ein wesentliches Kriterium dar.

Einfache, weitgenutzte vektorielle Strukturierungsansätze

Zur Komplexitätsreduktion wird in verschiedenen Standards und System¬implemen¬tierun-gen auf eine strenge topologische Modellierung verzichtet und bewusst eine Reduktion auf einfache geometrische Grundstukturen (simple features) vorgenommen. Mit der Simple Features Specification des Open Geospatial Consortiums (HERRING 2010, ANDRAE 2012) liegt ein Industriestandard für die Speicherung von Punkten und Punktmengen, Linien und Linienzügen sowie Polygonen und zusammengesetzten Elementen, wie z. B. Polygonen mit Enklaven, vor, dessen Implementierung als Bewertungskriterium im Systemauswahlverfahren herangezogen werden kann.

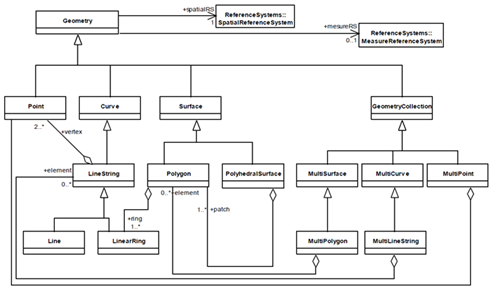
Die Spezifikation sieht verschiedene Geometrieklassen vor (vgl. Abbildung). Von einer allgemeine Klasse Geometry werden die Kindklassen Point, Curve, Surface (Oberfläche) und Geometry Collection (Sammlung von möglicherweise heterogenen Geometrieobjekten) abgeleitet.
MultiPoint, MultiCurve und MultiSurface sind von Geometry Collection abgeleitet. Sie sind spezialisierter und können jeweils nur Objekte einer Geometrieklasse aufnehmen.

Ein LineString (Linienzug) ist eine Spezialisierung der allgemeineren Curve-Klasse und kann eine einfache Linie (Line) oder ein LinearRing (geschlossener Linienzug) sein. Ebenso sind die Klassen Polygon und PolyhedralSurface (Vielflächner) von der Klasse Surface abgeleitet.

Auswerteverfahren

Für Vektordaten bieten die meisten GI-Systeme eine große Reihe spezifischer Auswerteverfahren:

• Geometrische Auswertungen: Geometrische Auswertungen stützen sich auf die Geometrie der Daten, d. h. sie basieren weitgehend auf Angaben zur Lage von Knoten sowie zur Form von Kanten. Zu ihnen zählen:
  • Auswertungen zu Grundflächen und Flächenanteilen,
  • Auswertung von Koordinaten oder Koordinatenbereichen,
  • Auswertung von geometrischen Lagebeziehungen wie Winkel und Abstandsmaße.
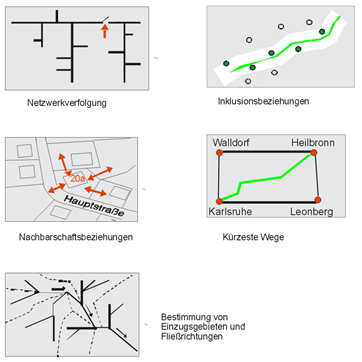
• Topologische Auswertungen: Zu den wesentlichen Analyseverfahren sind Auswertungen der Topologie zu zählen. Topologische Auswertungen benötigen in der Regel die Geometrie der Daten nicht, sondern basieren auf topologischen Verknüpfungen der Objekte untereinander. Zu nennen sind:
  • Auswertung von Nachbarschaftsbeziehungen,
  • Auswertung vollständiger oder teilweiser Inklusion,
  • Suche kürzester Verbindungen,
  • Abflussbestimmung.
• Auswertungen von Dreiecksnetzen: Aufbauend auf dem Dreiecksnetz sind u. a. folgende Analysen und Ableitungen möglich:
• Hanglänge, -neigung und -exposition,
• Hanglänge,
• Verschneidungen,
• Massenermittlungen,
• Interpolation von Isolinien.

Verknüpfung mit Attributdaten

Historisch gesehen lag bei vielen Systemansätzen das Hauptaugenmerk zunächst auf der Abbildung der geometrischen Eigenschaften. Knoten, Kanten und Maschen können jedoch auf verschiedene Weise um beschreibende Eigenschaften ergänzt werden. Dazu einige Beispiele.

Jede Fläche besitzt ein klassifizierendes, ganzzahliges Merkmal. Durch eine Transformation auf einen Wertebereich (Reklassifizierung) wird der eigentliche Attributwert gewonnen.

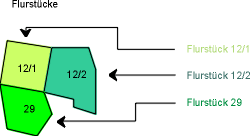
Verknüpfung Vektorgeometrie mit Attributen Den Flächen ist direkt ein Attribut - in diesem Fall eine Flurstücksnummer - zugeordnet.	Den Flächen ist direkt ein Attribut – in diesem Fall eine Flurstücksnummer – zugeordnet.
Jede Fläche besitzt ein klassifizierendes, ganzzahliges Merkmal. Durch eine Transformation auf einen Wertebereich (Reklassifizierung) wird der eigentliche Attributwert gewonnen.
Verknüpfung Vektorgeometrie mit Attributen	Mit geometrischen, topologisch verknüpften Geometrien ist über Schlüssel eine Attributtabelle verknüpft. Diesen Ansatz finden wir häufig bei CAD-basierenden Systemen; der Schlüssel stellt das Verbindungsglied zwischen Graphik und (relationaler) Datenbank dar.
Verknüpfung Vektorgeometrie mit Attributen	Für jedes Objekt werden Geometrie und alphanumerische, beschreibende Eigenschaften gemeinsam geführt.
Verknüpfung Vektorgeometrie mit Attributen über lineare Segmentierung	Bei der dynamischen Segmentierung werden unterschiedliche Attributsätze einem linienförmigen Objekt zugeordnet. Dabei ändern sich die Attributwerte längs des Weges.

Bewertung

Bezüglich des Einsatzes des vektororientierten Datenmodells ist auf folgende Gesichtspunkte hinzuweisen:

• Vektorbasierte Daten sind ideal für die Erfassung von Karten und Plänen sowie für vorwiegend kartographisch geprägte Anwendungen.
• Vektoren werden maßstabsunabhängig – allerdings immer nur in der Genauigkeit, die aus der Datenerfassung und den darauf folgenden Verarbeitungsschritten resultiert – gespeichert und können beliebig überlagert und kombiniert werden.
• Wegen fehlender Verfahren zur automatisierten Generalisierung sind dennoch häufig Daten unterschiedlicher Maßstäbe gesondert zu erfassen und zu speichern, wie es beispielsweise für die verschiedenen digitalen Landschaftsmodelle (DLM 25, DLM 100, …) beim Aufbau des Amtlichen topographisch-kartographischen Informationssystems (ATKIS) geschieht. Ein System muß heutzutage sowohl systemintern, als auch bei der Übergabe oder Abgabe von Daten topologische Strukturen unterstützen.
• Die Überlagerung vektorieller Information zur Datenverknüpfung ist ein komplexer und zeitintensiver Vorgang, da das System alle Schnittpunkte überprüfen und identifizieren muß. Dies bedeutet, daß diese Analyseart oft auf eine begrenzte Anzahl von Datensätzen eingeschränkt ist. Zusätzlich können sich aufgrund von Lageungenauigkeiten kleinere Restflächen ergeben, die in einem weiteren Bearbeitungsschritt zu eliminieren sind.
• Vektordaten liegen in vielen, unterschiedlichen Formaten vor. Dies führt zu erhöhtem Aufwand beim Austausch von Daten. Ein GIS sollte für wesentliche Vektorformate (amtliche und anbieterspezifische Austauschformate) Schnittstellen zur Verfügung stellen.